121. 霍奇闭链可以写成代数闭链的和吗？

Can a Hodge cycle be written as a sum of algebraic cycles?

题记：两种有用的数学结构在几何学(霍奇闭链)和抽象代数(代数闭链)中独立出现。霍奇猜想提出了它们之间一个令人惊讶的联系，但它们之间的这个桥梁到现在依然尚未完全建立。

一、代数闭链

0. 引言

1. 代数簇

2. 代数簇上的代数闭链

3. 代数闭链的等价关系

二、霍奇闭链

4. 复射影代数簇的丰富性质

前面我们讨论了代数簇X上的k 维代数闭链群C_(k) (X)及其等价类。代数闭链其实是代数簇X这个抽象几何体具有群对称几何结构的反映。前面已经提到如果X是一个光滑的复射影代数簇，那么它有更好的几何性质，即它可以被唯一地分解为有限多个不可约代数集的并集，而且其每一个不可约子代数集在闭集的意义下可以构成一个拓扑空间，称为扎里斯基拓扑(Zariski topology)。拓扑空间简单地来讲就是由集合X的子集为元素的一系列集族，而这些集族里的集合在集合交和并的运算下都保持封闭(集合是开集时集合交要求有限，集合是闭集时集合并要求有限)。显然代数簇X的所有子集满足拓扑的所有条件，故首先构成了一个拓扑空间。

由于霍奇猜想是建立在复射影代数簇上的，所以此处需要专门介绍一下复射影代数簇的数学性质。从霍奇猜想之一代数闭链的文章中我们已经知道，射影空间上的代数簇具有更加明确的代数几何特征(如在紧致的RP²空间中式(3)所定义的代数簇Z⁽²⁾ 的几何图像就是点)，而这些代数簇都是由闭数域上的齐次多项式函数环中的齐次理想所产生的(此处不必纠缠理想的概念，理想是环的重要子集，具有加法封闭性，乘法的吸收性，即理想中的元素乘以环中的任何元素都被吸收到理想中)，所以必然具有一定的拓扑结构(包含关系)，尤其对于复数域上的复代数簇(complex algebraic variety)它具有更好的拓扑性质。首先代数簇 Z^(m) (S) 是由多项式集合 S ⊆ K[x₁ , x₂ ,··· , x_m]的零解集给定的，而这些零解集可以看成 m 维空间上的点集，这些点集可以构成一个拓扑空间，对应一定的几何结构；而且一般情况下这些点集还会是连续的，如果代数簇不存在奇点，那么这些连续的点集还是光滑可微的，这样的代数簇最终会构成一个 m 维的实流形(manifold)M。所谓实流形M简单地讲就是：局部和欧几里得空间相似的拓扑空间 (也就是流形 M 上任何一点及其邻域都和 R^m 空间的单位开球拓扑等价)；其次，复数域 C 上的代数簇 Z^(m)(S) 还可构成一个复流形(complex manifold)(局部同构于C^m中的开集)，而这个复流形本身也具有一定的复解析结构，可以构成复拓扑流行，对应于非奇异的代数方程同时也会形成光滑的微分流行。如果在紧致化的复射影空间上，这个复的拓扑微分流形上每一点还都可以看做一个解矢量(它是m元多项式函数集合的零解集)并可以定义内积(对偶运算)，那么在内积上就会定义一定的内积测度(metric)，从而成为一个有测度的黎曼流行；又由于复空间中实部和虚部的反对称关系又使得m维复流形对应为偶数2m维的实流行并具有一定的辛结构，在其上可以引入外微分形式，又成为一种辛流行(symplectic manifold)。所以复射影代数簇可以同时是复流形、黎曼流形和具有辛结构的微分流形，此时它就被称为凯勒流形(compact Kähler manifold)，所以凯勒流形就是复流形、黎曼流形和辛流形的交集。反之，凯勒流形是一个具有凯勒结构(Kähler structure)的复流形，或者说凯勒流形具有凯勒形式(Kähler form)，它是一个辛流形，具有凯勒度量(Kähler metric)，所以它又是黎曼流形。总之，在一定的表象下凯勒流形对应的酉群表示应该是如下黎曼流形的表示 O(2m)、复流形的表示GL(m,C)和辛流形的表示 Sp(m) 的交集：

所以复射影空间上的代数簇可以对应于一个凯勒流形，它是集黎曼流形、复流形及辛流形三位一体的紧致微分流形，它显然是复代数簇在微分几何中的一个更为严格的推广。总之，复射影代数簇具有非常良好但也非常复杂的代数、几何、拓扑及微分结构，所以对于它的研究存在多个角度和方向，而霍奇猜想就是将复射影代数簇上的闭链结构和拓扑微分结构联系起来的桥梁。

5. 复射影代数簇的拓扑性质：同调和上同调

首先我们从拓扑的角度来分析复射影代数簇X的拓扑性质。对于拓扑空间数学家主要研究在连续形变下拓扑空间的不变性(所谓连续形变就是指形变中没有断裂点、相交点或粘合点)，而拓扑几何体所对应的拓扑不变性用拓扑不变量(topological invariants)来描述。由代数簇所决定的拓扑空间X上的连续变换对拓扑空间而言就是：不同的拓扑空间X和Y如果可以通过一个一对一的双射互相转变(同胚映射)，那么这两个拓扑空间就是拓扑等价的，称为拓扑同胚(homeomorphisms)，记为X ~ Y。拓扑空间连续双射所导致的同胚概念本质上是拓扑空间的某些几何结构在连续变换时不发生改变，比如拓扑空间的维度、紧致性、联通性等性质不发生改变，而这些不发生改变的性质，可以通过对应的不变量来反映，这些量就称为拓扑不变量，它们是用来判定两个拓扑空间是否等价的必要条件。然而拓扑空间的拓扑性质有多种，其中最基本的拓扑不变性有：紧致性 (封闭和有界的性质)、连通性(是否只有一个部分而不是多个独立部分的性质)以及豪斯朵夫 (Hausdorffness) 分离性(拓扑空间中点是否分离的)以及有向性(有没有内外的区分)等等。

在拓扑学中大家最为熟知的拓扑不变量就是：欧拉数。欧拉数的研究来源于图论中的哥尼斯堡七桥问题，主要的发现是由顶点(Vertice)和边(Edge)连接而成的图具有一个非常有意思的不变量：顶点数 V 减去边数 E 加上面数 F 等于一个数常数，如V - E + F = 2，三角形3个顶点减去3个边加上2个面(在紧致的空间中看三角形内部一个面加外部一个面)等于2。大家可以验证所有由顶点和边连接起来的连通图(不断开为几部分，如两个分立的三角形)这个数值都等于2。后来人们的研究发现这种性质对球面等二维闭连续曲面也成立，也是二维闭曲面的拓扑不变量。更进一步的研究又发现了欧拉数不是2的其他类型的拓扑曲面，并把曲面几何体的研究推广到了更加复杂的复合体上，也同时把欧拉数推广到了更高维，统一被称为欧拉示性数。

所以欧拉示性数是抽象拓扑空间上的拓扑不变量，为了更为清晰地认识欧拉示性数的广泛意义，根据多面体欧拉数的规律可以在一个更加抽象和简单的拓扑空间上引入欧拉数的概念。这个简单的拓扑空间就被称为单纯复形(simplicial complex)，而这个单纯复形的欧拉数可以通过更为广义的同调理论(cohomology theory)来表达，所以同调可以反映拓扑空间或流形的整体性质，它是欧拉数的一个更为精细化的描述。而对于单纯复形上的欧拉数，它可以这样定义：由于单纯复形是由更基本的单元“单形(simplex)”组成，所以一个单纯复形的欧拉数 χ  为

其中 c_k 为单纯复形中k-单形(k-simplex)的个数。k-单形(k-simplices)是由k维空间k + 1 个点连接而成的最简单的几何体，记为σ^(k)，它本质上是由k + 1个线性不相关的 k 维点 v_i 组成的一个点集所决定的几何体,用数学语言定义为：

以上的定义(10)表明k-单形是通过k + 1个 k 维顶点连接而成的一个凸形(凸多面体)，所以对由 k+1 个彼此线性独立的顶点组成的 k-单形可以直接表示为：σ^(k) ≡ {v₀ , v₁ , v₂ ,··· , v_k}，它被顶点唯一定义，维度是 k，其几何图像的概念只依赖于顶点的个数和维度，和位置大小没有关系。比如1-单形为线段，你移动旋转(甚至拉伸)它都表示1-单形；2-单形为三角形，3-单形为正四面体，都可以任意平移旋转(拉伸)都代表同样的2-单形和3-单形，依此类推。由于k-单形{v₀ , v₁, v₂,··· ,v_k}顶点排列顺序的改变虽然不改变单形的几何图像，但其方位(如转动)是不同的，为了固定单形的方位(方向)，引入有向k-单形(oriented k-simplices)的概念。一个单形的方向可以用生成其顶点的一个排列来表示(用圆括号表示)，某个排列的奇次置换会改变方向，而偶次置换彼此等价。这样在有向单形上就可以引入有向单形的边界。显然有向k-单形对应 k 维空间一个凸几何体，而它的边界应该是k −1 维的有向单形，所以我们定义有向 k-单形的边界算子为：

根据以上的边界算子的定义很容易证明：对于任意的有向k-单形有 ∂² σ^(k)≡ ∂_k−1∂_k σ^(k) = 0。

对于一个更加复杂的几何体，单形可以根据边界按照一定的规则粘合成一个单纯复形。图1给出了由单形组合生成的复形的几何图像。如图1(a)所示单形按照边组合构成了一个单纯复形，它显然由4个0维的0-单形σ⁽⁰⁾(顶点v₀,v₁,v₂,v₃)，4个1维的1-单形σ⁽¹⁾(就是边)，1个2维的2-单形σ⁽²⁾(面)按照它们的边界粘合而成，所以其欧拉数可简单计算为：4 - 4 + 1 = 1；而图1(b)所给的图形不是单纯复形(因为没有很好地按边界粘合,顶点4在面的内部，单形没有按边界粘合)，当然也可以定义其欧拉数，但一般不研究此类有边相交的图形；最后图1(c)所给的单纯复形的边是有方向的，称为有向单纯复形，它的欧拉数为：4 - 5 + 1 = 0。此时这些由式(9)给出的欧拉数可以对应或相当于单纯复形的一个三角剖分，所以复形的欧拉数就可以用三角剖分的图形所对应的顶点数(0-单形)减去边数(1-单形)加面数(2-单形)减体(3-单形)等等的数目来计算，在三维空间中公式(9)就完全对应于欧拉公式V - E + F 给出的欧拉数计算公式。

图1 单纯复形的示意图

然而如果复形成为一个连续的拓扑空间即流形，那它将对应一个超曲面，而这个超曲面可以通过一个三角剖分(不唯一)对应于一个单纯复形，从而也存在相应的欧拉数。所以通过欧拉数可以区分不同的拓扑空间或连续曲面，比如球面的欧拉数 χ = 2，环面的欧拉数χ = 0等等。一般地对于一个曲面如果它的亏格(genus)为g时(亏格可以简单理解为曲面上的洞的个数)，有向面的欧拉数：χ =  2 − 2g，而无向面的欧拉数：χ =  2 − g。欧拉示性数还能揭示流形的几何性质与分析性质之间的深刻联系。例如，一个曲面的总曲率就等于其欧拉示性数，这便是高斯-博内定理，而在高维情形下这个定理也同样成立；另一引人注目的结果是庞加莱-霍普夫定理，该定理将欧拉示性数与向量场的总指数(total index)等同起来，从而对流形上可能存在的向量场类型给出了限制的条件。这种全局分析与拓扑学之间的相互关联总能让人发现激动人心的结果，其中最有力的体现如著名的阿蒂亚-辛格指标定理：该定理通过上同调类(cohomology classes)确定了自旋流形上狄拉克算子的解析指数(analytic index),该定理给出了微分算子的解析性质与流形的拓扑结构之间本质的联系。

根据以上的关于单纯复形上的拓扑性质分析，我们在其上引入同调理论(homology theory)。所谓的同调其实就是指拓扑空间和欧拉数或曲面亏格有关的概念。同调(homology)的英文意思为“相同性”，而中文之所以被翻译为“同调”，因为其和几何体上的“洞”相关。比如一个笛子，堵住不同的洞其实就是改变了笛子上洞的数目，这样笛子的音调也就不同，所以可以通过分析几何曲面上的洞来研究抽象几何体的拓扑性质。那如何去统计和刻画这些洞来对拓扑空间进行分类或研究呢？这就是同调理论需要解决的问题。数学上同调其实就是依靠洞来分类，分类的依据是通过抽象几何体上的映射来实现的。当然分类不能用“同构”这种非常“精细”的映射，而需要引入“同态映射”的概念。所谓同态(Homomorphism)表达了不同代数系统(algebraic system)之间的某种相似关系(similar form)，它不同于拓扑空间上的同胚映射。同态能在不同代数系统之间定义，代数系统指在其元素上定义了某种运算关系的集合，比如群、环、域、矢量空间等。

假设两个代数系统 G 和 H，其上分别定义了运算 ◦ 和 ∗，则两个代数系统通常记为(G,◦) 和(H,∗)。如果它们之间存在映射ϕ : G → H 满足 ϕ(g₁ ◦ g₂ ) = ϕ(g₁ ) ∗ ϕ(g₂)，其中g₁, g₂∈ G; ϕ(g₁) ≡ h₁, ϕ(g₂) ≡ h₂; h₁, h₂ ∈ H，那么这两个代数系统通过 ϕ 建立了同态关系。同态给出了不同代数系统之间的映射和运算可以相互交换的关系，即先运算后映射等于先映射后运算，显然二者的结构是相似的。如果同态映射 ϕ 是满射(onto)，即 H 中元素在 G 都有对应的原像，这种同态映射被称为满同态(epimorphism)；如果同态映射 ϕ 还是一对一的单射(injection)，即 G 中不同的元素在 H 中有不同的像，称为单同态 (monomorphism)；更重要的一种同态就是映射ϕ: G → H 既是单射还是满射(injection and onto)，也就是所谓的一对一的双射(bijection: ϕ 存在逆映射)，此时同态映射就成为同构映射(同构符号为 ≌ )，显然同构比同态更为精细一些。

图2 同态映射的核和像示意图

同态映射给出的不同代数系统的相似度比同构更粗略，同态映射既是单射又是满射的时候才是同构，所以同态能给出代数系统之间一个“分类”，这就涉及到同态映射的两个重要概念：像(image)和核(kernel)。如果两个代数系统是群或具有群结构，那么同态映射通过其像和核可以对群进行分类。如图2所示，同态映射 ϕ: G → H 的像定义为：im(ϕ) = {h ∈ H : h = ϕ(g), g ∈ G}，此即G在H上的像；同态映射ϕ: G → H 的核定义为：ker(ϕ) = {g ∈ G : ϕ(g) = 1_H }，此即群 G 映射到群 H 单位元1_H的所有元素的集合。群同态有个基本定理：G/ker(ϕ) ≌ im(ϕ)。这个定理的意思是群 G关于同态核的商群G/ker(ϕ)和像 im(ϕ)是同构的。由此可见同态映射的核可以作为群G的不变子群对群G的元素进行分类(共轭类)，每一个共轭类组成的集合将G分解为与像同构的商群。显然群的一个同态映射会将群同构分解，这将看到群结构中更为细节的东西，然而不同的同态映射给出的群分类将是不同的，这就如同代数闭链阿贝尔群上的不同等价类。对于具有群结构的拓扑空间利用同态核进行分类的方法最好存在一个有限的映射过程，而这就需要利用适当的同态映射找到一个递减或递增的链群结构，所以在单纯复形上我们首先要找到一个链群（复形）序列。

由于单纯复形X是由公式(10)定义的不同维度的k-单形{σ^(k), k = 0, 1, 2, ···}以一定的数量按照边界组合而成的几何体(比如三角形是由三个点和三个边组合而成)，因此我们可以在单纯复形X上先定义一个k-链(k-chain)。对于单纯复形X上不同的k维单形 {σ_i^(k), i = 0, 1, ···}，我们把某个“由不同有向 k-单形的整系数线性组合而构成的元素”称为该单纯复形空间的一个k-链(k-chain)，而所有k-链组成的集合则构成一个加法群或线性空间，称为k-链群，记为 C_(k) (X)：

在k-链群上我们需要引入合适的同态映射，这个同态映射将建立不同维k-链群之间的映射关系，这样的映射可以让k-链群的维度减小(如微分)，也可以让其维度增加(如积分)，为了让其有效截断，我们引入边界同态映射：

边界算符是一个具有微分性质的运算，如果X是一个复代数闭链群，那其上的边界运算就决定了一个复代数闭链群的同态映射关系，这个关系具有如下的映射降链结构：

显然这样的降链C_*最终会被边界映射退化到0，我们将这样的链群链称为链复形(chain complex),可记为(C_*, ∂_*)。我们根据边界作用在有向k-单形上的性质，可以发现这样的边界映射作用在k-链群上有一个重要性质：∂_k−1 ∂_k  C_(k) (X)=  0，也就是说任何链的边界的边界为零。这样k维链的边界∂_k C_(k) 就组成k-1维的闭链群，它一定是链群C_(k-1)的边界链的子群，也就是这个子群中的所有链的边界都一定等于零，这样我们推广一下把所有边界映射为零的链称为闭链(cycle)。假如边界映射为零的闭链的维度为 k，则称为k-闭链(k-circle)，所有的k-闭链的整系数线性组合也组成一个加法阿贝尔闭链群Z_(k)(X)，显然Z_(k)(X)群也是链群C_(k) (X)的子群。

图3 边界同态映射的关系图

根据前面同态映射的概念参照图3所示，闭链群Z_(k)(X)就是边界同态映射 ∂_k 的核：Z_(k) = ker(∂_k )(注意加群的单位元就是0)；而又根据同态像的定义，同态映射 ∂_k+1 的像记为：B_(k)≡ im (∂_k+1) ⊆ C_(k) (X)，显然 B_k 中所有 k 维链都是k维边界闭链，因为同样有 ∂_k B_(k) = 0，所以群B_(k)是一个边界闭链群，简称 k 维边界链群。边界链群是一类特殊的闭链群，也就是边界群B_(k)一定是闭链群，但闭链群Z_(k)不一定是边界链群，所以B_(k)是Z_(k)的子群：B_(k) ⊆ Z_(k) ⊆ C_(k)。这样我们在链群上就可以定义如下的商群：

而我们把公式(15)所定义的商群即称为链群C_(k)上的k-维同调(k-dimensional homology)，或者称为链复形(C_*, ∂_*)的第k-阶同调模(k-th homology module)。显然同调群可以刻画有多少闭链不能构成边界，也就是有多少个“洞”使得闭链无法构成边界。进一步，如果空间是连续的非奇异的闭流形M(对应闭的有向的光滑几何超曲面)，那么这个流形M可以通过一个有向的三角剖分来计算其欧拉数，其即为该流形上三角剖分后k维单形的同调群H_(k)(M)秩(rank)的轮换和：χ = rank H₍₀₎(M) - rank H₍₁₎(M) + rank H₍₂₎(M) - rank H₍₃₎(M) + ··· , 其中rank H₍₀₎(M)表示点同调群的秩、rank H₍₁₎(M)表示边同调群的秩等等，具体群秩的概念可参考科学问题120，此处的上同调群的秩就等于拓扑空间独立洞的个数。这里涉及到一个定理：一般系数定理(Universal Coefficient Theorem)，它可以证明k-单形上整系数链群的同调群的秩等于一般系数(上面(12)式所定义的链群的系数不再是整数Z而是在任意的数域K中取值，比如有理数、实数、复数等)链群上同调群的维数：dim H_(k)(M; K) = rank H_(k)(M; Z)。注意此处的复形可以对应到一个光滑流形，它也是一个拓扑空间，其上存在如上所述的链复形(chain complex)，此时所涉及的链群根据定义链系数的数域K不同可称为K链群，如有理链群、实链群或复链群等等。

根据上面的表述，定义同调群的链复形具有降链结构(维数降低)，如果将以上的链采用其相对应的对偶链(如余维链)，则以上的降链复形就变成上链复形(Cochain Complex),而此时采用上指标，对偶的上链复形可以记为(C^*, ∂^*)，对偶的边界同态映射则变为：∂^k+1 : C^k → C^k+1，其他的都保持不变，则此时第k-阶上同调群(k-th cohomology group)定义为：

建立在单纯复形上的经典同调和上同调都能反映一个流形或拓扑空间的整体性质，但反映的方式不同，一个通过拆分而一个通过积分来表达。上同调有两个基本特征：首先它只依赖于拓扑空间的洞(与单位元0元素有关，或由典型的边界路径，或者由同伦homotopy的概念来界定，此处不想牵扯太多概念，从略)，当然这也是同调的特征；其次是它可以由局域“数据”决定，这就决定了上同调可通过局部的微分性质来计算。显然同调和上同调捕捉拓扑空间“洞”的方式不同，同调理论的目标似乎是检测空间中的闭链是否能形成边界，而上同调的目标是检测空间函数在闭链上是否可积。这种刻画洞的不同方式也表现在图3所示的同态映射决定链复形的方向性上，它们之间的关系在一般拓扑空间上会显得复杂(由一般系数定理给出)，但在m维定向闭流形M上，同调群H_(k)(M)和上同调群H^(m-k)(M)彼此同构(庞加莱对偶定理)。所以同调可以认为是用空间结构所生成的阿贝尔群C_(k)来刻画洞的方式，即主要的关注点是单纯复形的组合结构，可以用来计算洞的个数和维数(如贝蒂数 Betti number，见后面内容)，物理上同调理论多用于计算DNA的缠绕数或流体拓扑中计算流体洞如涡旋的拓扑不变量；而上同调则通过定义于空间上函数的行为来间接探测洞的性质，可以通过函数在洞上的积分更为精细地刻画空间的结构(比如它存在比群更复杂的环结构)，可以用空间的局域微分结构计算(微分形式的上同调)，从而更广泛地应用于物理学的各个领域(如电磁场的微分表述形式、规范场理论等)。

 建立在单纯复形拓扑空间上的上同调可以称为经典上同调，而如果我们允许单纯复形中单形的边或面等“部件”可以任意弯曲或拉伸，此时的单形就成为奇异单形(Singular Simplex)，而由奇异单形构成的链则变成了奇异链(Singular Chain)，而由奇异链构成的复形就被称为奇异链复形(Singular Chain Complex)，此时由单形构成单纯复形就可以通过连续地形变(连续映射)对应到一个拓扑空间M，而这个拓扑空间上的上同调则被称为奇异上同调(Singular Cohomology)，一般记为：H_sing^(k)(M, K),其中K表示链的系数取值数域(比如有理链)。显然，奇异上同调来源于所研究几何体的连续性，它从由点和边的简单图形转变成了连续的几何拓扑空间，比如光滑流形M，从而经典的上同调理论被推广为奇异上同调理论。然而由于光滑流形上还具有微分结构，使得它的上同调理论又增加了新的微分几何结构特征，这就是德拉姆上同调理论(de Rham cohomology theory)。

6. 流形上的微分结构和德拉姆上同调

根据前面讲的复射影代数簇 X 的性质，X 不仅是一个拓扑空间，还可以是一个光滑的流形 X → M，而在这个光滑的流形上存在一个很好的微分结构。由于X 是一个光滑的复射影代数簇，它的复维度dim_C(X) = m，那么它将对应复射影空间中一个连续的抽象几何体，它的每一点处都光滑(没有奇点)可以构成一个复微分流形。由于复微分流形上存在多种不同的定义链复形序列的方式，所以存在复杂的上同调理论。根据单纯复形上拓扑空间的性质，此时组成单纯复形拓扑空间的单形，其顶点之间就可以用随意弯曲的线连接并进一步成为一个连续的流层，而此时单纯复形就是由这些层流组成。显然这些不同维的层流所组成的拓扑空间，具有良好的微分结构。在光滑流形 M上我们可以通过微分形式引入上同调群，此时的边界算子就成为其上的微分形式，闭链就成为微分的闭形式，上链就是由不同微分形式(积分或边界微分关系)形成的链序列，从而此时引入的上同调就称为德拉姆上同调(de Rham cohomology)。

下面我们介绍光滑流形上的外微分形式及其上建立的德拉姆上链复形(de Rham cochain complex)，然后给出德拉姆上同调概念。为了简单，我们先在闭的有方向的 m 维光滑实流形 M 上讨论，然后再推广到复流形上，所以我们先引入实流形的外微分形式。在 m 维实流形 M 上取一个点p∈M，其坐标记为 (x_p1 , x_p2 , ··· , x_pm)，那么其沿着某个坐标轴方向的微元的坐标(dx_p1 , dx_p2 , ··· , dx_pm)就是该点切空间的坐标，可以用来展开 p 点的切空间矢量。根据前面的讨论，光滑流形是由不同维度的层流组合而成的，所以我们可以在其上引入 k 维层流形里的k次外微分形式：dx₁ ∧ dx₂ ∧ ··· ∧ dx_k，这种微分形式称为外微分形式(exterior differential form)是因为它们满足这样的方向关系：dx_i∧dx_j = −dx_j∧dx_i。此时这里的 k 次外微分形式就等价于前面讲的有向 k-单形(无限可微的微单形)。所以在流形的每一点 p 处(为方便标记把点的记号用 j 表示)会存在这样一个局域的k维外微分切空间：(dx_j1, dx_j2, ··· , dx_jk )，而 j 点邻域的微分结构就能表示为如下的线性组合：

这就称为外微分的k-形式(k-form)，其中展开系数 f _j (p) 的函数值在此处已经不同于单纯复形链的系数在整数域Z取值了(见(12)式)，它可以在实数域R上取值(即为实流形上的实函数)。当然 f _j 也可以在有理数域Q或复数域C上取值，这种不同系数的外微分有时会利用下标标出。

同样所有的k-形式ω^(k)在加法运算下会组成一个加法阿贝尔群，记为Ω^k(M,R)，默认在实流形上时简写为 Ω^k (M)，而这个群的所有元素ω^(k)在加法和数乘(实数)下是封闭的，所以群Ω^k (M)又是一个实线性空间(实矢量空间)。根据外微分的计算法则我们就有不同外 k 维外微分群Ω^k (M)上的一个外微分(exterior derivative)映射 d : Ω^k (M) → Ω^k+1(M)。这个线性映射会形成一个和式(14)一样的上链群序列，称为德拉姆上链复形(de Rham cochain complex)：

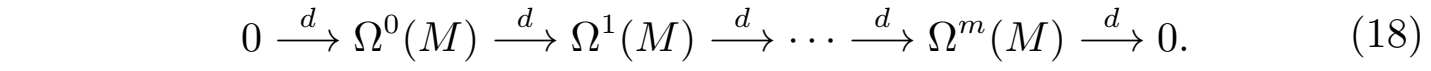
外微分d满足和前面单形边界算子相同的性质：d ² = 0，也就是对任意k-形式ω^(k)∈Ω^k (M)，都有d²ω^(k)=0。同样，我们把dω^(k)=0的k-形式ω^(k)称为闭形式(对应单纯复形上的闭链)，所有的闭形式组成一个群Z^k，显然它是映射d的核：Z^k = ker( d: Ω^k (M) → Ω^k+1(M) )；同理，如果对于k-形式ω^(k)如果存在(k-1)-形式ω^(k-1)使得ω^(k)=dω^(k-1)，那么k-形式ω^(k)就被称为恰当形式(exact form)，对应于前面单纯复形的边界链。所有的k-恰当形式组成一个恰当群B^k，显然B^k是外微分映射d的像：B^k = im( d: Ω^k-1(M) → Ω^k(M) )。根据外微分运算d ² = 0的性质，闭形式一定是恰当的，所以有：B^k(M) ⊆ Z ^k(M) ⊆ Ω^k(M)。于是非常自然地就可以在德拉姆上链上引入德拉姆上同调群：

其中H_dR^(k)(M, R) 就被称为定义于实微分流形M上的第k阶德拉姆上同调群(k-th de Rham cohomology group)。对于一般的 m 维光滑流形或所有闭流形M，其上的任意 k 阶德拉姆上同调群的维度dim(矢量空间的维数)都是有限的：dim H_dR^(k)(M) = dim Z^k − dim B^k < ∞，这样我们把 k 阶德拉姆上同调的维数用 β_k (M)表示，即β_k (M) = dim H_dR^(k)(M)，而β_k (M)则被称为第 k 阶贝蒂数(k-th Betti number)，它刻画了流形 M 上有几个 k 维洞，而所有贝蒂数的轮换和即为欧拉数：

显然此处在微分流形上计算欧拉数已经不需要对流形进行几何三角剖分了，只需要计算流形上的贝蒂数(不同维洞的个数)就可以了。

现在我们把 m 维实流形 M 直接推广到 m 维复流形X。流形从实数域推广到复数域显然直接可以将 m 维实流形上一点 p ∈ M 直接复数化，此时p邻域的坐标自然写为：(z₁, z₂ , ··· , z_m )，其中z_j = x_j + i y_j, x_j 和 y_j 分别表示实部和虚部。显然这种推广是将局域的 R^m 直接推广为 R^m ⊗ C，此时m维复流形将直接等价于 2m 维的实流形，其对应的 k 次外微分自然变为：dz₁∧dz₂∧ ···∧dz_k∧dz₁ ∧dz₂∧ ··· ∧dz_k ，其中z_j 表示z_j 的复共轭坐标z_j =x_j - i y_j，并且 dz_j = dx_j − i dy_j ，显然dz_j∧dz_j= (−2i)dx_j∧dy_j ，这样所有的外微分都变成了实的外微分，只是此时的系数可以在复数范围内取值。所以这样对于外微分算子 d 作用于实数化的k 阶外微分形式(实虚部都统一用dx 表示)：

其中f _{j1,j2 ,···,jk} 在复数域中取值，是复流形 X 上的复变函数，外微分结果将是k +1阶外微分形式。所有的ω_C^(k)组成一个加法群或复矢量空间Ω_C^k (X)，这样外微分算子d将给出一个态映射d : Ω_C^k (X) → Ω_C^k+1 (X)，依然有d² = 0。所以外微分算子d 自然给出和式(18)一致的由外微分形式群上的d算子给出的复形序列：

这样外微分d算符的闭形式和恰当形式分别为群Ω_C^k (X)的子群，这样就可以根据链复形序列式(22)定义复系数的德拉姆上同调群：

显然在直接推广的复流形 M ⊗ C → X ≌ R^m ⊗ C上的德拉姆上同调群H_dR^(k)(X, C)是式(19)定义的实德拉姆上同调H_dR^(k)(M, R)的直接复化，也就是将式(17)定义的实系数的外微分形式直接改为复系数的外微分形式式(21),所以它们之间的关系为：H_dR^(k)(X, C) ≌ H_dR^(k)(M, R)⊗C。这里有一个重要的德拉姆定理：对于任意的光滑流形 X，复系数的德拉姆上同调群H_dR^(k)(X, C)同构于复系数的奇异上同调群H_sing^(k)(X, C)。而且复系数德拉姆上同调群H_dR^(k)(X, C)和有理系数的奇异上同调群H_dR^(k)(X, Q)之间也存在如下同构关系：H_dR^(k)(X, C) ≌ H_sing^(k)(X, Q) ⊗_Q C。

然而由于复空间的微分结构中实部和虚部存在一定的联系，也就是复空间存在对偶性，这就为复微分结构带来了更为丰富的结构特征，所以它并不是简单地把m维复空间对应为2m的实空间，或只将外微分的系数从实数变为复数。前面推广的复外微分形式：dz₁∧dz₂∧ ···∧dz_k∧dz₁ ∧dz₂∧ ··· ∧dz_k 其实是一个2k次的复系数的实外微分形式，它没有包含复坐标及其共轭坐标外微分的区分，为了更清楚地显示复坐标及其共轭坐标的外微分次数，可以将如上的 k 形式记为(k, k)形式。而对于该形式可以进一步推广为如下的 (p, q) 形式：dz₁∧dz₂∧ ··· ∧dz_p ∧ dz₁ ∧dz₂∧ ··· ∧dz_q，注意此时的外微分中复坐标的外微分次数p已经不再与共轭(对偶)坐标的外微分次数q相等了，这种外微分形式已经不是定义于复流形上同一层点的复空间的邻域内，它可能是不同层点某个共同邻域上的(p, q)形式。所以一般复流形 X 上任意点 p 邻域上的(p, q)型外微分形式可定义为：

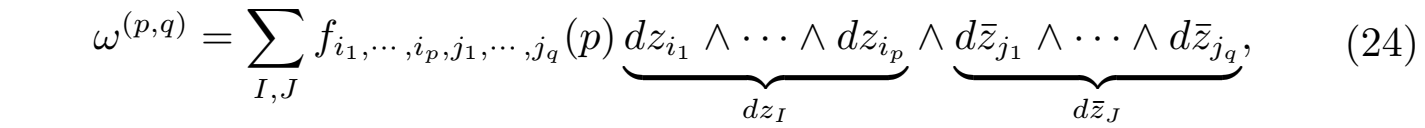
其中 I ≡ (i₁, i₂ , ···, i_p),J ≡ (j₁, j₂,···, j_q)，而 f_{i1, i2 , ···, ip, j1, j2,···, jq}(p) = f _I,J (p) 是定义于复流形 X 上的无限可微的复变函数： f _I,J (p) ∈ C^∞ (X,C)。由于复坐标的微分其复坐标和共轭坐标的微分的变换规则是相互分离的，所以(p, q)型外微分形式具有坐标变换不变性，和坐标的选择无关，具有整体性。那么复流形上的复结构导致复化的外微分算子d 可以分解为两个算子之和：d = ∂ + ∂，其中算子∂ 也被称为多尔博算子(Dolbeault operator)，它的作用结果为 ∂ : Ω^(p,q) (X) → Ω^(p+1,q) (X)，也就是它只对形式中的全纯坐标分量 z 进行微分，从而只“提升”p 指标，满足∂ ² = 0；同样，算子∂ 称为反多尔博算子(anti Dolbeault operator)，其作用结果为 ∂ : Ω^(p,q) (X) → Ω^(p,q+1) (X),它只对形式中的全纯坐标分量的复共轭 z 进行微分，从而只“提升”q 指标，满足∂ ² = 0，而且这两个算子的混合外微分也等于零：∂ ∂ = ∂ ∂ = 0，这就预示着前面讲的外微分算子：d² = (∂ +∂)² = 0 自然成立。所以外微分算子d作用在(p, q)型外微分形式上的结果为 d : Ω^{(p, q)} (X) → Ω^{(p+1, q)} (X) ⊕ Ω^{(p, q+1)} (X)。

图4 算子∂和算子∂所给出的链复形阵列

根据多尔博算子的性质，利用算子∂和∂都能构造(p, q)型上的链复形序列(此处为如图4的序阵列)，从而定义相应的上同调群。显然沿着横向行方向的链复形可用来定义∂上同调：

同理，沿着竖直列方向也可以定义∂上同调：

所以我们利用算子∂和∂的阵列映射关系选择不同的链复形映射方向可以定义不同的上同调群，比如采用上面d算子和其共轭算子d^†的和(d + d^†)，或者利用图4中红色箭头的映射方式，等等，此处上同调的复杂性来源于微分流形复空间结构的复杂联系，总之利用算子∂和∂定义的上同调群都可以称为多尔博上同调群(Dolbeault cohomology)，一般H_∂^{(p, q)}(X)被称为多尔博上同调群，因为它是实流形上德拉姆上同调在复流形上的自然推广。然而多尔博上同调群和德拉姆上同调的关系极为复杂，比如从维度上看式(26)所定义的多尔博上同调与德拉姆上同调的维度之间有如下关系：

更进一步，由于复矢量空间具有对偶性，可以在复矢量空间上根据对偶性定义内积测度，从而这样的复流形就成为前面提到的凯勒流形。在复射影簇所对应的紧致凯勒流形上，对于任意的正整数 k，凯勒流形X上的上同调具有以下的正则分解(canonical decomposition)：

以上的分解就是著名的霍奇分解(Hodge decomposition)，它将凯勒流形上的k 阶德拉姆上同调分解为一系列(p,q)型上同调群H^{(q, p)}(X, C)的直和，也就是凯勒流形上的k阶上同调空间可分解为(或同构于)一系列(p,q)型上同调子空间的直和。比较式(27)和式(28)可以发现，正因为流形上引入了对偶测度(凯勒测度)造成的测度使得(p,q)型上同调群H^{(q, p)}(X, C)具有对偶关联，导致了H^{(q, p)}(X, C)上同调与多尔博上同调群的区别(具有调和性)，显然(p, q)型上同调群H^{(p, q)}(X, C)的共轭对形式即为H^{(q, p)}(X, C)，即有：。

7. 霍奇闭链

最后我们给出霍奇闭链的概念。假设X是紧致的凯勒流形，那其上的霍奇闭链α_k 就是如下集合内的元素(类)：

可见霍奇闭链其实是复德拉姆上同调群H_dR^(2k)(X, C)和(p,q)型上同调群H^{(k, k)}(X, C)交集的元素，它显然是上同调群中复外微分形式中特殊的上同调类，所有霍奇闭链α_k的集合即霍奇类可以记为Hdg^(k)(X)，代表着复微分流形空间的微分结构中特殊的对角型外微分形式，这种特殊的外微分结构实际是特殊的调和形式(harmonic form)。式(29)中(p,q)型H^{(p, q)}(X, C)上同调类元素的调和外微分是在拉普拉斯椭圆微分算子∆下等于零的边界闭链：∆ ω_C^(k)= 0，而式(29)中的德拉姆上同调群也可以通过如下的调和形式定义：

其中∆ = dd^† + d^†d 就是霍奇拉普拉斯算子(Laplacian)，这个算子的具体含义我们将在第三部分再具体介绍，而公式(30)中的Ω_C^k (X)即为(21)式所定义复k阶微分形式空间。所以德拉姆上同调类H_dR^(k)(X, C)具有独特的调和形式表象，而霍奇闭链是一类具有特殊对称结构的上同调类。

霍奇闭链α_k的上同调类一开始是定义在整数霍奇闭链上的猜想，即公式(29)中外微分形式的系数在整数域Z中取值，公式(29)中上同调为H_dR^(2k)(X, Z)和H^{(k, k)}(X, Z)，但后来发现这个猜想并不正确(有反例)，于是将霍奇闭链改为有理数霍奇闭链，于是目前(29)式中的C改为了有理数域Q。所以目前的霍奇猜想是寻找定义在复射影代数簇上的有理霍奇闭链和代数闭链之间到底有什么样的对应关系，我们将在第三部分霍奇猜想中再详细进行介绍。

* 形成本文的参考资料和文献涉及了大量不同类型的论文、讲座和视频等材料，非常抱歉此处无法详细罗列，特此说明。